Boxing corners tutorial

NOTE: found some mistakes here, so the changes are in red=)

Welcome to the “all-the-information-you-ever-wanted-to-know-about-boxing-corners” tutorial. I’ve included several different ways to box corners as well as how to design them and have them turn out the right dimensions. I’ve tried to make it clear, but it’s easy to get confused (happened to me LOTS! see Brain Strain and Ready, set, sew!), so leave me a comment if you need more help, okay?!

Let’s start by learning how to sew a boxed corner. (Of course, if you are just dying to know how the algebra works, just click on one of the links below and you’ll magically leap to that section =)

The two main methods of boxing corners are what I’m calling the “cut-out method” and the “folding method”. With both of these methods you can start out with two separate pieces of fabric that get sewn together, or you can have one piece of fabric that gets folded over.


The cut-out method
The folding method.
The cut-out method, the algebra.
The folding method, the algebra.

The cut-out method

This is the easier of the two methods, involving only two steps.
1. Once you’ve sewn the side and bottom seams, clip the corners and refold the bag (right sides together) so that the side seam matches up with the bottom seam. (If you are starting with one piece of fabric, just guesstimate where the bottom seam would be.)

the tan box is using one piece of fabric and the other uses two pieces

2. Sew a line perpendicular to the bottom seam, usually a ¼” seam allowance is sufficient. (Some people like to sew another line 1/8” into the seam allowance for sturdiness.)

That’s it, your corner is boxed! Easier that you thought, huh? You can also check this link for more pics on the cut-out method of boxing corners. The pics are about halfway down the post. They are thumbnails, but clicking on them will give you more detail

Back to top

The folding method

1. Once you’ve sewn the side and bottom seams, clip the corners and refold the bag (right sides together) so that the side seam matches up with the bottom seam. (If you are starting with one piece of fabric, just guesstimate where the bottom seam would be.)

the tan box is using one piece of fabric and the other uses two pieces (sorry about the squiggly lines!)

2. Make sure that the amount on the left side of the seam is the same as the amount on the right. It might be necessary to readjust the fabric.
3. Measuring from the point, make a mark that is half the desired size of the box. For example, if you want your box to be 5” deep, then make your mark 2 ½” up from the point. Make sense?
4. Now draw a line perpendicular to the seam line at the mark and sew along this line. (Some people like to sew another line 1/8” into the seam allowance for sturdiness.)

note that both the blue and pink lines are the same length. (purple=seam line, red=stitching line) (you'll probably need to click on the pic to see the detail)

5. Trim close to the seam line.

That’s it, your corner is boxed!

Back to top

Cut-out algebra

Now, suppose you want to design your own project with the “cut-out” boxed corner method, how do you know how much fabric you need? Here’s how you figure it out.

Starting with one piece of fabric
Starting with two pieces of fabric
Starting with one piece of fabric and folding

One piece of fabric – (you’d use this method if you were designing a pocket, for example)
CAVEAT: this is the version that is the trickiest for me. I’ve gotten it figured out, but I still look at the formula at times and go “huh? what? how did I get that?” so don’t worry if it doesn’t seem to make sense. Just know that it works out in the end!!

Here are the measurements that you’ll need:
– A = finished width of box
– B = finished height of box
– C = raw edge folded in
– D = depth of box
– E = seam allowance for the box
– F = fold over (this is totally optional, it just makes for a nicer looking pocket)
– G = width of fabric to cut
– H = height of fabric to cut
– I = vertical cut for notch
– J = horizontal cut for notch

These are the magic formulas:
A + (D x 2) + (E x 2) + (C x 2) = G
B + F + E + D = H
D + E = J
D = I

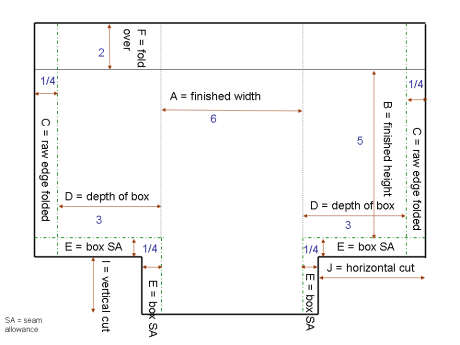
Here’s an example using the drawing above.
A = 6 inches
B = 5 inches
C = ¼ inch
D = 3 inches
E = ¼ inch
F = 2 inches

So plugging in the numbers, here’s what you end up with:
6 + (3 x 2) + (¼ x 2) + (¼ x 2) = 13 (this is G)
5 + 2 + ¼ + 3 = 10¼ (this is H)
3 + ¼ = 3¼ (this is J)

So you’ll want to cut your fabric 13 x 10¼
You’ll want to cut a notch in each lower corner that is 3 inches tall and 3¼ inches wide.

Back to top Back to cut algebra

Two pieces of fabric – (you’ll use this method if you will be sewing a seam at the bottom of the purse/bag/etc.)

Here are the measurements that you’ll need:
– A = finished width of box
– B = finished height of box
– C = seam allowance
– D = depth of box
– E = seam allowance for the box
– F = top seam allowance (used if you are attaching lining or if you’ll fold under the raw edge)
– G = width of fabric to cut

– H = height of fabric to cut

– I = vertical cut for notch

– J = horizontal cut for notch

These are the magic formulas:
A + (E x 2) + D + (C x 2) = G
B + F + E + (D/2) + C = H
(D/2) + C – E = J
J = I

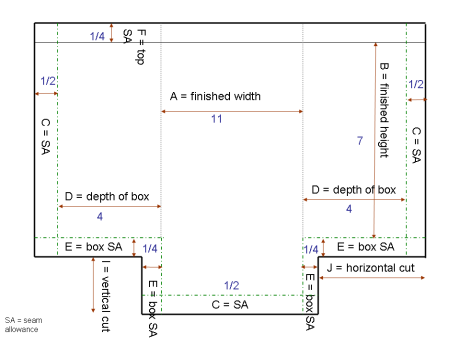
Here’s an example using the drawing above.
A = 11 inches
B = 7 inches
C = ½ inch
D = 4 inches
E = ¼ inch
F = ¼ inches

So plugging in the numbers, here’s what you end up with:
11 + (¼ x 2) + 4 + (½ x 2) = 16½ (this is G)
7 + ¼ + ¼ + (4/2) + ½ = 10 (this is H)
(4/2) + ½ – ¼ = 2¼ (this is both J and I)

So you’ll want to cut your fabric 16½ x 10
You’ll want to cut a notch in each lower corner that is 2¼ inches tall and 2¼ inches wide.
NOTE: The depth of your box will actually end up being be the seam allowance for the box (E), which is ¼ inch in our example. I know it has to do with the box seam allowance, I just haven’t figured out how to account for that. But I figure ¼ inch is no biggie, it could be chalked up to a cutting or measuring error. If you have an idea on how to solve this, let me know! Hooray! DH helped me figure this out, so you’ll notice the new and improved formula. BUT, given the nature of how this particular box works, if your measurements are off at all (seam line isn’t exactly right, fabric isn’t perfectly straight, etc), the box will end up being either bigger or smaller than intended. *SIGH*

Back to top Back to cut algebra

One piece of fabric that is folded – (you’ll use this if you WILL NOT be sewing a seam at the bottom of the purse/bag/etc.)

Here are the measurements that you’ll need:
– A = finished width of box
– B = finished height of box
– C = seam allowance
– D = depth of box
– E = seam allowance for the box
– F = top seam allowance (used if you are attaching lining or if you’ll fold under the raw edge)
– G = width of fabric to cut
– H = height of fabric to cut
– I = vertical cut for notch
– J = horizontal cut for notch

– K = where to make the horizontal cut for the notch

These are the magic formulas:
A + (E x 2) + D + (C x 2) = G
(B x 2) + (F x 2) + (E x 2) + D = H
(D/2) + C – E = J
D – (E x 2) = I
(H – I)/2 = K

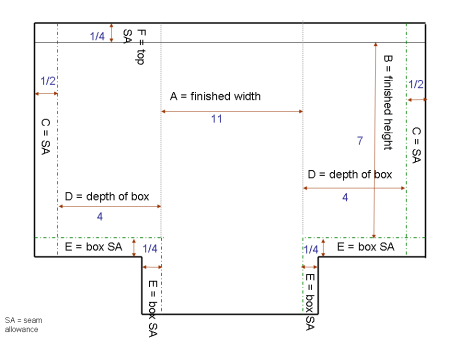
Here’s an example using the drawing above.
A = 11 inches
B = 7 inches
C = ½ inch
D = 4 inches
E = ¼ inch
F = ¼ inches

So plugging in the numbers, here’s what you end up with:

11 + (¼ x 2) + 4 + (½ x 2) = 16½ (this is G)

(7 x 2) + (¼ x 2) + (¼ x 2) + 4 = 19 (this is H)

4 – (¼ x 2) = 3½ (this is I)

(4/2) + ½ – ¼ = 2¼ (this is J)

¼ + 7 + ¼ = 7½ (this is K) (19 – 3½)/2 = 7 3/4 (this is K)

So you’ll want to cut your fabric 16½ x 19

You’ll want to cut a notch 7 3/4 inches from each end that is 3½ inches tall and 2¼ inches wide.

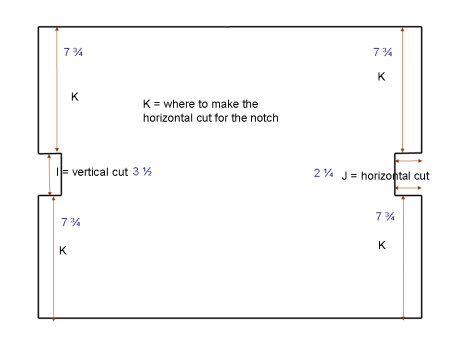
NOTE: The depth of your box will actually end up being be the seam allowance for the box (E), which is ¼ inch in our example. I know it has to do with the box seam allowance, I just haven’t figured out how to account for that. But I figure ¼ inch is no biggie, it could be chalked up to a cutting or measuring error. If you have an idea on how to solve this, let me know! Hooray! DH helped me figure this out, so you’ll notice the new and improved formula. BUT, given the nature of how this particular box works, if your measurements are off at all (seam line isn’t exactly right, fabric isn’t perfectly straight, etc), the box will end up being either bigger or smaller than intended. *SIGH*

Back to top Back to cut algebra

Folding algebra

If you are designing your own project with the “folding” boxed corner method, here’s how you figure out your fabric needs. (Of the two methods, this is definitely the easiest one to design!)

Starting with one piece of fabric
Starting with two pieces of fabric

One piece of fabric

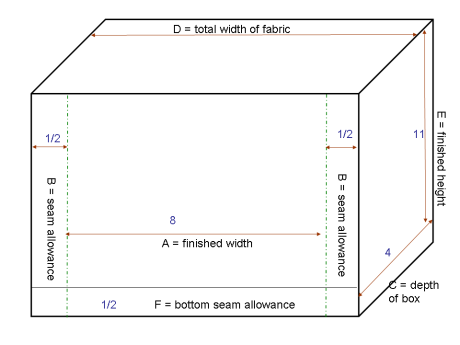
Here are the measurements that you’ll need:
– A = finished width of box
– B = seam allowance
– C = depth of box
– D = width of fabric to cut
– E = finished height of box
– F = height of fabric to cut

These are the magic formulas:
A + (B x 2) + C = D
C + (E x 2) = F

Here’s an example using the drawing above.
A = 8 inches
B = ½ inch
C = 4 inches
E = 11 inches

So plugging the numbers in, here’s what you end up with:
8 + (½ x 2) + 4 = 13 (this is D)
4 + (11 x 2) = 26 (this is E)

So you’ll want to cut your fabric 13 x 26
NOTE: you’ll need to add more to the height if you’ll be making a casing or will be folding over the raw edges.

Back to top Back to folding algebra

Two pieces of fabric
CAVEAT: You can do this method with two pieces of fabric, but I’ve found that it works better to start with one and fold it in half.

Here are the measurements that you’ll need:
– A = finished width of box
– B = seam allowance
– C = depth of box
– D = width of fabric to cut
– E = finished height of box
– F = bottom seam allowance
– G = height of fabric to cut

These are the magic formulas:
A + (B x 2) + C = D
(C/2) + E + F = G

Here’s an example using the drawing above.
A = 8 inches
B = ½ inch
C = 4 inches
E = 11 inches
F = ½ inch

So plugging the numbers in, here’s what you end up with:
8 + (½ x 2) + 4 = 13 (this is D)
(4/2) + 11 + ½ = 13 ½ (this is F)

You’ll want to cut each piece of fabric to be 13 x 13 ½
NOTE: you’ll need to add more to the height if you’ll be making a casing or will be folding over the raw edges.

Back to top Back to folding algebra

Wow! You made it through all of that . . . .CONGRATS! You should now have a really good handle on how to sew and design boxed corners. If you have any questions or problems, leave me a comment and we’ll tackle it together! Happy boxing!! =)